Una de las cosas que más disfruté en la universidad fue analizar e implementar algoritmos desde cero. Hoy quiero repetir ese ejercicio con un algoritmo extremadamente útil a la hora de resolver problemas.
Existen cientos de algoritmos de ordenamiento, todos con sus pros y sus contras. Creo que todos nos hemos topado con ese video en YouTube que muestra de manera gráfica cómo funcionan.
¿Qué es un algoritmo de ordenamiento?
Aunque sea bastante auto explicativo e incluso se pueda entender claramente solo viendo el video de arriba, no quiero dejar cosas sueltas.
Un algoritmo de ordenamiento es aquel cuyo propósito es ordenar los elementos de una lista, sean números (orden numérico) o letras (orden lexicográfico, el que utilizan los diccionarios).
El orden resultante puede ser ascendente o descendente, según nuestra implementación, es decir, según lo que necesitemos.
Entendiendo el algoritmo Merge Sort
La base para entender este algoritmo, y tantos otros, es comprender la idea detrás del “divide y vencerás”, uno de los paradigmas más importantes de la algoritmia, que “traducido” a la programación se conoce como método recursivo o recursión.
Este concepto tan importante se utiliza cuando nos enfrentamos a problemas grandes con soluciones complejas; en vez de intentar resolverlo como un todo, lo que hacemos es dividir ese problema en subproblemas más pequeños que se puedan resolver de forma casi trivial, para luego unir todas esas soluciones en una solución universal.
Método recursivo: dividir un gran problema en subproblemas más pequeños que se puedan resolver de forma trivial, para luego unir todas esas soluciones en una solución universal
Pero vamos a ponerlo en un ejemplo práctico.
Supongamos que tenemos el siguiente arreglo de 10 números y queremos ordenarlos de menor a mayor:
Siguiendo la idea de “divide y vencerás buscamos dividir el problema hasta llegar a uno tan pequeño que se pueda resolver trivialmente, así que empecemos dividiendo en arreglo en dos.
Como es un arreglo de 10 elementos y 10 dividido 2 es 5, vamos a tener dos arreglos de 5 elementos.
Bien, pero el problema sigue siendo grande y no existe solución trivial, así que continuamos dividiéndolo.
En el siguiente paso tenemos que dividir entre 2 un arreglo de 5 elementos, como es un número decimal vamos a tomar solo la parte entera (2), por lo que tendremos un arreglo de 2 y otro de 3 elementos.
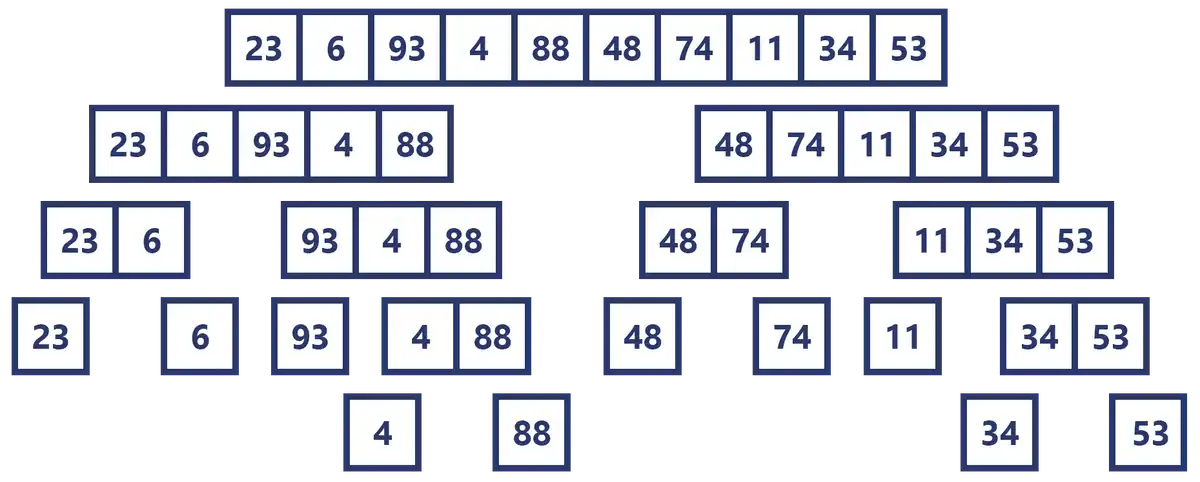
Si repetimos este proceso hasta no poder simplificar más el problema, inevitablemente vamos a terminar con 10 arreglos de 1 elemento cada uno.
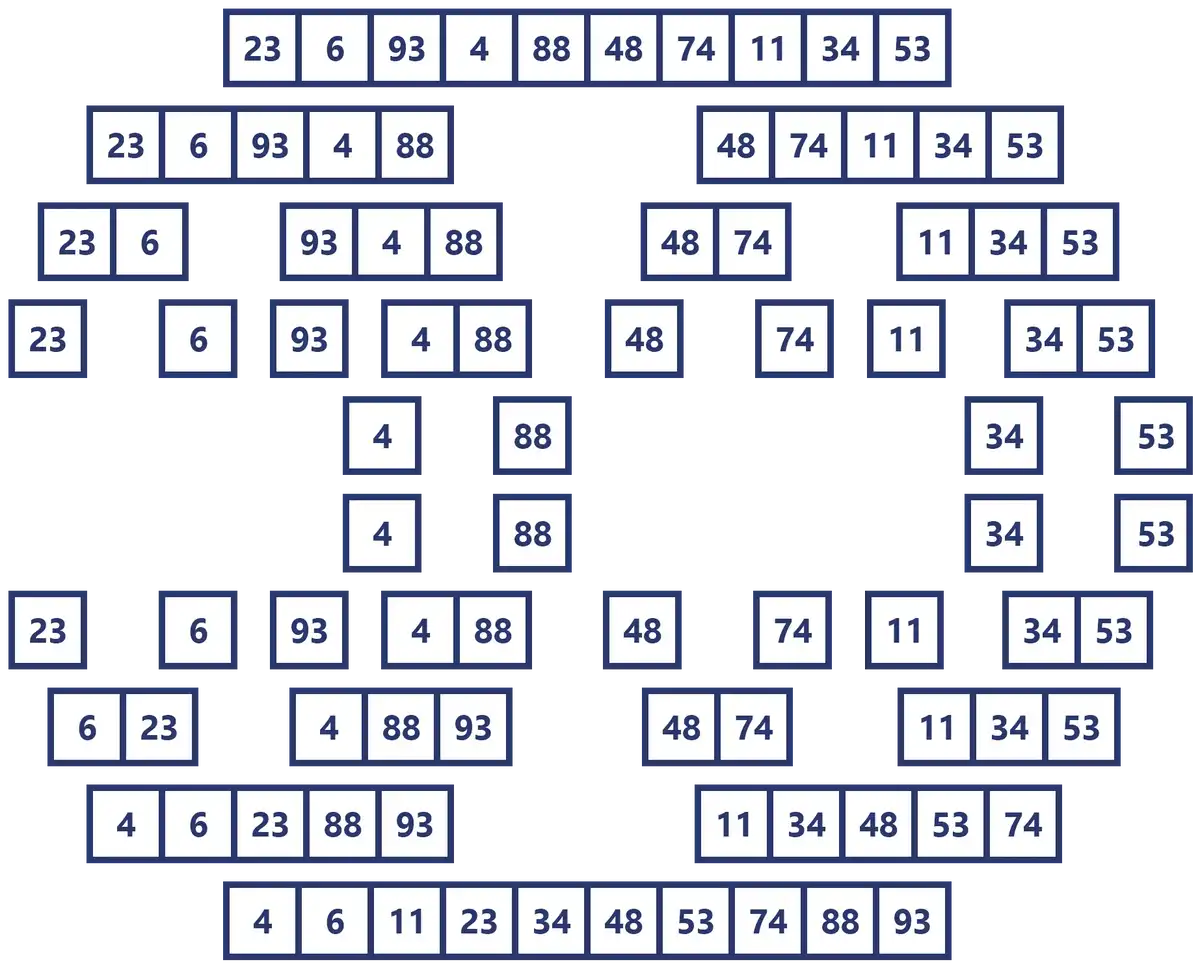
Visualmente el proceso entero sería el siguiente:
Pongámoslo en código paso por paso
Antes de escribir código siempre me hago estas dos preguntas.
¿Qué tiene que hacer nuestra función? Recibir un arreglo como parámetro y devolverlo ordenado.
¿Qué es lo que necesitamos hacer? Necesitamos dividir el arreglo hasta que tengamos un solo elemento, para posteriormente ordenarlo.
Acabamos de definir nuestro caso base, es decir, la condición para detener la recursión.
Empecemos por escribir eso. Para evitar condicionales anidados voy a escribir mi código utilizando Guard Clauses.
const mergeSort = (array) => {
// Si nuestro arreglo tiene un solo elemento ya no hay que dividirlo.
// Este es nuestro caso base, simplemente retornamos el arreglo.
if (array.length <= 1) return array
//
// Lógica para ordenar el arreglo...
//
}Ahora tenemos que dividir el arreglo en dos, para eso utilicé el método slice() propio de los arreglos en JavaScript.
Este método acepta dos parámetros opcionales, el primero es la posición inicial donde va a comenzar a ‘copiar’ el arreglo, el segundo parámetro es la posición final.
Si no se especifica el segundo parámetro, se copiará hasta el final del arreglo. Y si no se especifica ningún parámetro, se copiará todo el arreglo.
Lo importante de este método, a diferencia del método splice() es que éste último modifica el arreglo original.
Sabiendo cómo funcionan ambos métodos podemos escribir nuestro código de la siguiente manera:
const mergeSort = (array) => {
if (array.length <= 1) return array
// middle es nuestro "pivot", que es el elemento que está a la mitad del arreglo
// Utilizar ~~ es equivalente a Math.floor()
const middle = ~~(array.length / 2)
const left = array.slice(0, middle)
const right = array.slice(middle)
//
// Lógica para ordenar el arreglo...
//
}Ya dividimos el arreglo en dos, pero nos falta lo más importante: la recursión.
Y hacerlo es lo más sencillo de todo, pero puede llegar ser lo más abstracto de entender.
Simplemente tenemos que volver a dividir el arreglo en dos, y ya escribimos toda la lógica para hacerlo en esta misma función, así que lo único que tenemos que hacer es volver a llamar a mergeSort() con las dos mitades del arreglo como parámetro.
Este código se va a ejecutar hasta llegar al caso base, es decir, hasta que tengamos un arreglo de 1 elemento.
const mergeSort = (array) => {
if (array.length <= 1) return array
const middle = ~~(array.length / 2)
// Llamamos a mergeSort() con las dos mitades del arreglo como parámetro
const left = mergeSort(array.slice(0, middle))
const right = mergeSort(array.slice(middle))
//
// Lógica para ordenar el arreglo...
//
}Cómo ordenar recursivamente el arreglo
Ya logramos dividir nuestro arreglo al máximo posible, ahora nos toca ordenar los elementos.
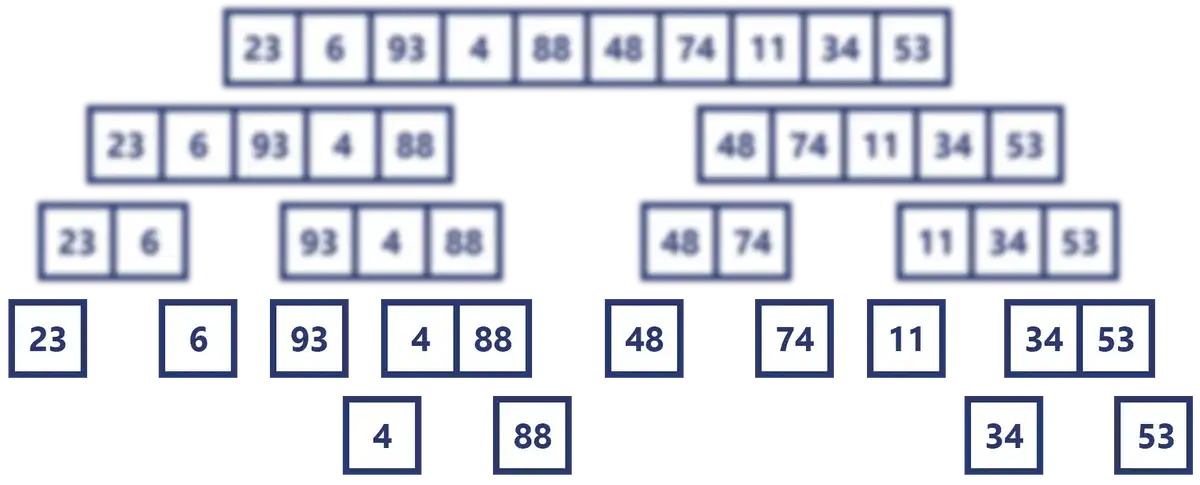
Esta es la parte más abstracta de la recursión, así que quiero graficarla bien para que no haya mucho lugar a dudas, así que volvamos a la última imagen y concentrémonos en las últimas dos filas.
Podemos ver que [23] y [6] son los primeros arreglos de 1 solo elemento, y vienen justamente de dividir el array [23, 6], por lo que [23] va es la parte izquierda, y [6] la derecha.
Nuestra misión ahora es ordenar estos dos arreglos y unirlos de nuevo en uno solo.
La lógica para resolver esto es simple, podemos crear un arreglo e ir insertando los elementos según el orden que nosotros queramos, en este caso lo vamos a hacer de forma ascendente.
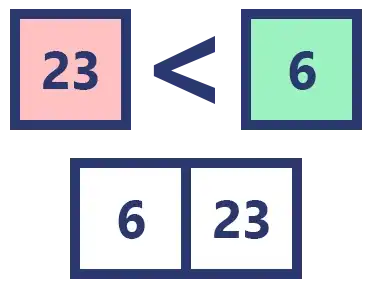
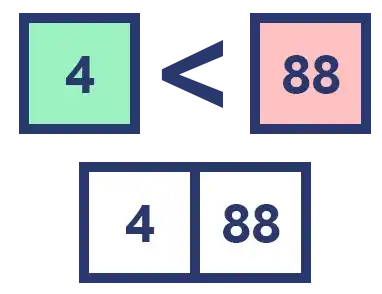
Comparamos 23 con 6. Como 6 es menor que 23 lo insertamos primero, y como ya no hay más elementos para comparar simplemente insertamos el 23 que sobra.
Este caso es el más simple, sólo estamos comparando dos elementos, así que veamos un ejemplo más.
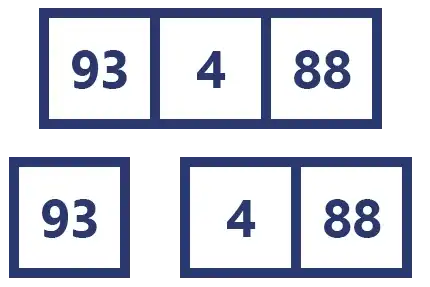
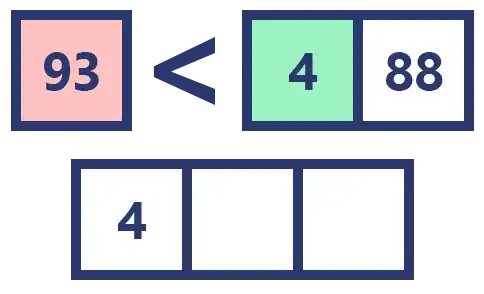
En esta ocasión tenemos a un arreglo [93, 4, 48] que se dividió en dos, [93] y [4, 48].
Siguiendo la lógica planteada con el ejemplo anterior tendríamos que comparar los valores que hay dentro de cada uno de los arreglos para ir insertando los menores en un nuevo arreglo.
Pero en realidad el arreglo [4, 48] aún no ha terminado de dividirse, recordemos que estamos en una función recursiva donde el caso base es que el arreglo tenga un solo elemento, así que nuestra función va a dividir y a ordenar este arreglo antes de compararlo con otro.
Exactamente igual que antes, comparamos los valores y los insertamos en orden en un nuevo arreglo.
Casualmente ya estaban ordenados, pero de más está decir que no siempre es así, sobre todo teniendo en cuenta que el orden (ascendente o descendente), lo elegimos nosotros.
Ahora sí podemos ordenar estos dos arreglos.
A pesar de que sean de diferente tamaño la lógica para ordenar es siempre la misma.
Comparamos los elementos y los vamos insertando en orden. 93 > 4, por lo que insertamos el 4 primero.
Al insertarlo ya nos podemos olvidar de ese 4, ya no hay que compararlo con ningún otro elemento.
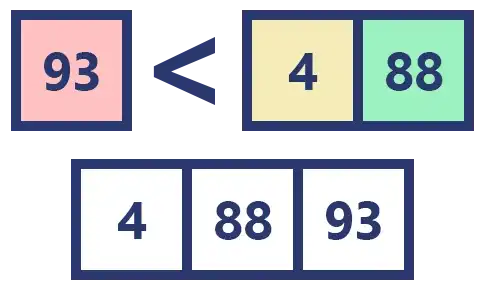
Pasamos a la siguiente comparación. 93 > 88, por lo que insertamos el 88.
Ya no hay más elementos para comparar, así que insertamos el 93 que sobra.
Este proceso se va a repetir hasta que todas las “piezas” del arreglo se hayan ordenado y se hayan unido en una sola.
Entendiendo este proceso con código
Ya escribimos nuestra función mergeSort() que se encarga de dividir. Ahora tenemos que crear otra función para ordenarlos, para eso vamos a repetirnos las preguntas que nos hicimos antes.
¿Qué tiene que hacer nuestra función? Recibir dos arreglos como parámetro y devolver un arreglo con los elementos de estos ordenados.
¿Qué es lo que necesitamos hacer? Necesitamos recorrer los arreglos que recibimos como parámetros y comparar los valores de sus elementos para finalmente insertarlos en un nuevo arreglo ordenado.
Hay diferentes maneras de realizar esta tarea. Una es utilizando el método shift(), pero este método al igual que splice() modifican el arreglo al que se le aplica, así que primero voy a explicar cómo hacerlo sin modificar el arreglo original.
const sort = (left, right) => {
// Creo un arreglo vacío que va a ir almacenando los elementos en el orden correcto
const sortedArray = []
// Estas variables las utilizo para saber qué índice del arreglo estoy recorriendo
let leftIndex = 0, rightIndex = 0
// Mientras tenga elementos en al menos uno de los arreglos tengo que seguir comparando elementos
while (leftIndex < left.length && rightIndex < right.length) {
// Comparo los elementos de los arreglos
if (left[leftIndex] < right[rightIndex]) {
// Determiné que el número menor es el de left[leftIndex]
sortedArray.push(left[leftIndex])
// Ya no necesito comparar ese número, por lo que aumento en 1 su índice
leftIndex += 1
} else {
// Determiné que el número menor es el de right[rightIndex]
sortedArray.push(right[rightIndex])
// Ya no necesito comparar ese número, por lo que aumento en 1 su índice
rightIndex += 1
}
}
// Retornamos el arreglo ordenado
return sortedArray
}Utilizando el método shift(), que sí modifica el arreglo al que se le aplica, el código queda más corto:
const sort = (left, right) => {
// Creo un arreglo vacío que va a ir almacenando los elementos en el orden correcto
const sortedArray = []
while (left.length > 0 && right.length > 0) {
// Busco el menor elemento de los dos arreglos
// El método shift() retorna el primer elemento del arreglo y lo elimina del original
// Es por eso que la condición del while es que al menos uno de los dos arreglos tenga elementos
if (left[0] < right[0]) sortedArray.push(left.shift())
else sortedArray.push(right.shift())
}
// Retornamos el arreglo ordenado
return sortedArray
}Estos códigos funcionan bien, pero hay un problema.
En los dos casos la condición de salida de la iteración es que hayamos terminado de recorrer uno de los arreglos.
Esto quiere decir que aún quedan elementos en el arreglo que no terminamos de recorrer.
Afortunadamente no tenemos que pensar mucho en qué hacer con el resto de los elementos. Por la lógica de nuestro algoritmo recursivo es seguro que los elementos que no hayamos recorrido se encuentren en el orden correcto (tal y como vimos con imágenes en el segundo ejemplo), por lo que solo tenemos que agregarlos al arreglo ya ordenado.
Esto podemos hacerlo simplemente concatenando los arreglos a través del método concat() , pero a partir del punto en el que dejamos de explorarlos, algo que sabemos gracias al valor de las variables leftIndex y rightIndex.
En código sería así:
const sort = (left, right) => {
const sortedArray = []
let leftIndex = 0, rightIndex = 0
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] < right[rightIndex]) {
sortedArray.push(left[leftIndex])
leftIndex += 1
} else {
sortedArray.push(right[rightIndex])
rightIndex += 1
}
}
// Uno de los dos va a ser un arreglo vacío
// Pero no nos interesa descartarlo, por lo que concatenamos ambos
return sortedArray.concat(left.slice(leftIndex)).concat(right.slice(rightIndex))
}Si no nos importó modificar el arreglo original podemos hacerlo como lo hicimos en el código anterior pero sin pasarle ningún parámetro a slice().
O bien podemos usar ”array destructuring”, de la siguiente manera:
const sort = (left, right) => {
const sortedArray = []
while (left.length > 0 && right.length > 0) {
if (left[0] < right[0]) sortedArray.push(left.shift())
else sortedArray.push(right.shift())
}
// Nuevamente uno de los dos arreglos estará vacío
// Pero es justamente porque está vacío que no es necesario descartarlo
return [...sortedArray, ...left, ...right]
}Y con estas dos simples funciones ya tendríamos las piezas necesarias para implementar Merge Sort en JavaScript.
Al final el proceso que va a seguir nuestro código se va a ver algo así:
El código completo en el caso de que no se quiera modificar el arreglo original es:
const mergeSort = (array) => {
if (array.length <= 1) return array
const middle = ~~(array.length / 2)
const left = mergeSort(array.slice(0, middle))
const right = mergeSort(array.slice(middle))
return sort(left, right)}
const sort = (left, right) => {
const sortedArray = []
let leftIndex = 0, rightIndex = 0
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] < right[rightIndex]) {
sortedArray.push(left[leftIndex])
leftIndex += 1
} else {
sortedArray.push(right[rightIndex])
rightIndex += 1
}
}
return sortedArray.concat(left.slice(leftIndex)).concat(right.slice(rightIndex))
}Y el código completo en el caso de que no nos importase modificar el arreglo original es:
const mergeSort = (array) => {
if (array.length <= 1) return array
const middle = ~~(array.length / 2)
const left = mergeSort(array.slice(0, middle))
const right = mergeSort(array.slice(middle))
return sort(left, right)}
const sort = (left, right) => {
const sortedArray = []
while (left.length > 0 && right.length > 0) {
if (left[0] < right[0]) sortedArray.push(left.shift())
else sortedArray.push(right.shift())
}
return [...sortedArray, ...left, ...right]
}En ambos casos no nos tenemos que olvidar de llamar a la función sort() dentro de la función mergeSort().
¿Por qué usar Merge Sort?
La ventaja de Merge Sort por sobre otros algoritmos de ordenamiento más básicos es su corto tiempo de ejecución.
Es uno de los algoritmos de ordenamiento más rápidos y eficientes, con un Big-Θ de Θ(n*log(n)) incluso en el peor caso.
¿Cuál es el peor caso?
Al ejecutar Merge Sort no necesariamente se tienen que comparar todos los elementos para ordenarlos, porque al terminar de recorrer y ordenar un subarreglo (la condición de salida de nuestro bucle) podemos dar por sentado que el resto de los elementos ya están ordenados y agruparlos (es decir, concatenarlos como en nuestro código).
Con esto en mente podemos inferir que el peor caso será cuando nuestro algoritmo tenga que hacer todas las comparaciones posibles.
Un ejemplo sería el arreglo [0, 2, 4, 6, 1, 3, 5, 7].
Pueden hacer el proceso en esta página y verán que el algoritmo siempre va a tener que comparar los elementos entre sí para poder ordenarlos.
¿Cuándo utilizar Merge Sort?
Hay una parte importante de este algoritmo que hemos estado haciendo, y es que para lograr que funcione estamos creando nuevos arreglos en donde insertamos los elementos en el orden deseado.
Esto puede ser un problema si tratamos con una enorme cantidad de datos y puede que lo mejor sea utilizar otro algoritmo como Quick Sort o Heap Sort.
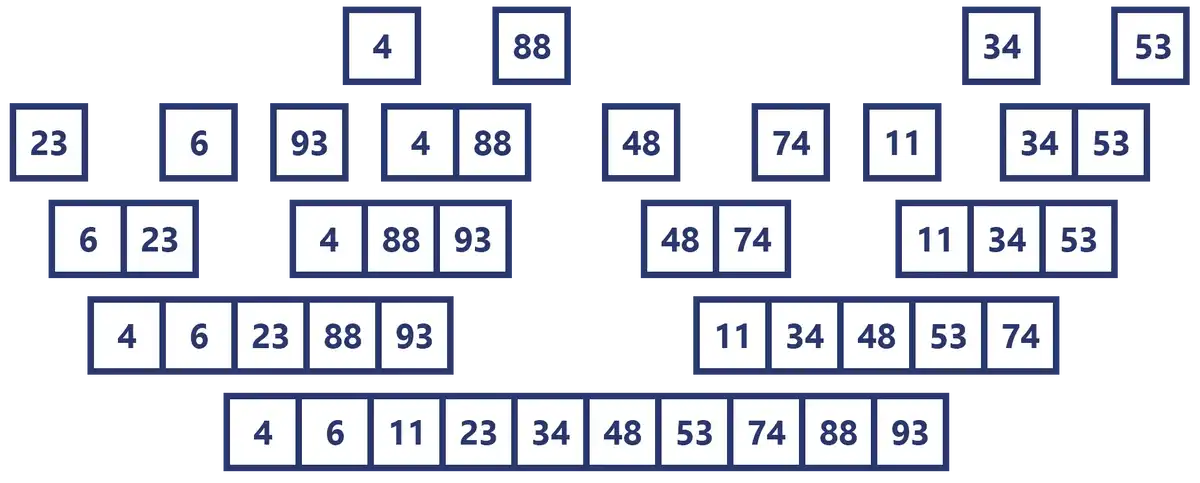
El proceso completo del algoritmo Merge Sort en una imágen
Mientras iba realizando este artículo terminé con una imagen de esta forma algo curiosa, así que la comparto para finalizar el tema.
Conclusión
Merge Sort es un algoritmo de ordenamiento muy eficiente incluso en el peor caso, pero requiere una gran cantidad de espacio de memoria adicional para funcionar. Esto hace que no sea una muy buena opción cuando se trata con una gran cantidad de datos; pero en el caso contrario es una excelente alternativa en contraste con los demás algoritmos de ordenamiento.