One of the things I enjoyed most in college was analyzing and implementing algorithms from scratch. Today I want to repeat that exercise with an extremely useful algorithm when solving problems.
There are hundreds of sorting algorithms, all with their pros and cons. I think we’ve all come across that video on YouTube that graphically shows how they work.
What is a sorting algorithm?
Although it’s pretty self-explanatory and can even be clearly understood just by watching the video above, I don’t want to leave things loose.
A sorting algorithm is one whose purpose is to sort the elements of a list, whether they are numbers (numerical order) or letters (lexicographic order, the one used by dictionaries).
The resulting order can be ascending or descending, according to our implementation, that is, according to what we need.
Understanding the Merge Sort Algorithm
The basis for understanding this algorithm, and so many others, is to understand the idea behind “divide and conquer”, one of the most important paradigms of algorithmics, which “translated” to programming is known as recursive method or recursion.
This very important concept is used when we are faced with large problems with complex solutions; instead of trying to solve it as a whole, what we do is divide that problem into smaller sub-problems that can be solved in an almost trivial way, and then unite all those solutions into a universal solution.
Recursive method: Breaking a large problem down into smaller sub-problems that can be solved trivially, with the purpose of joining all those solutions into a universal solution.
But let’s put it into a practical example.
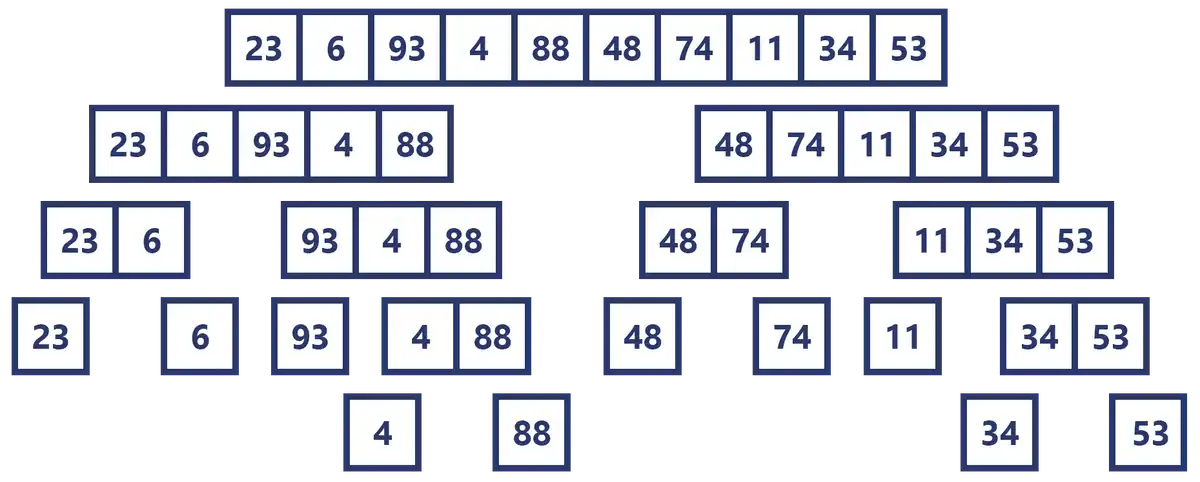
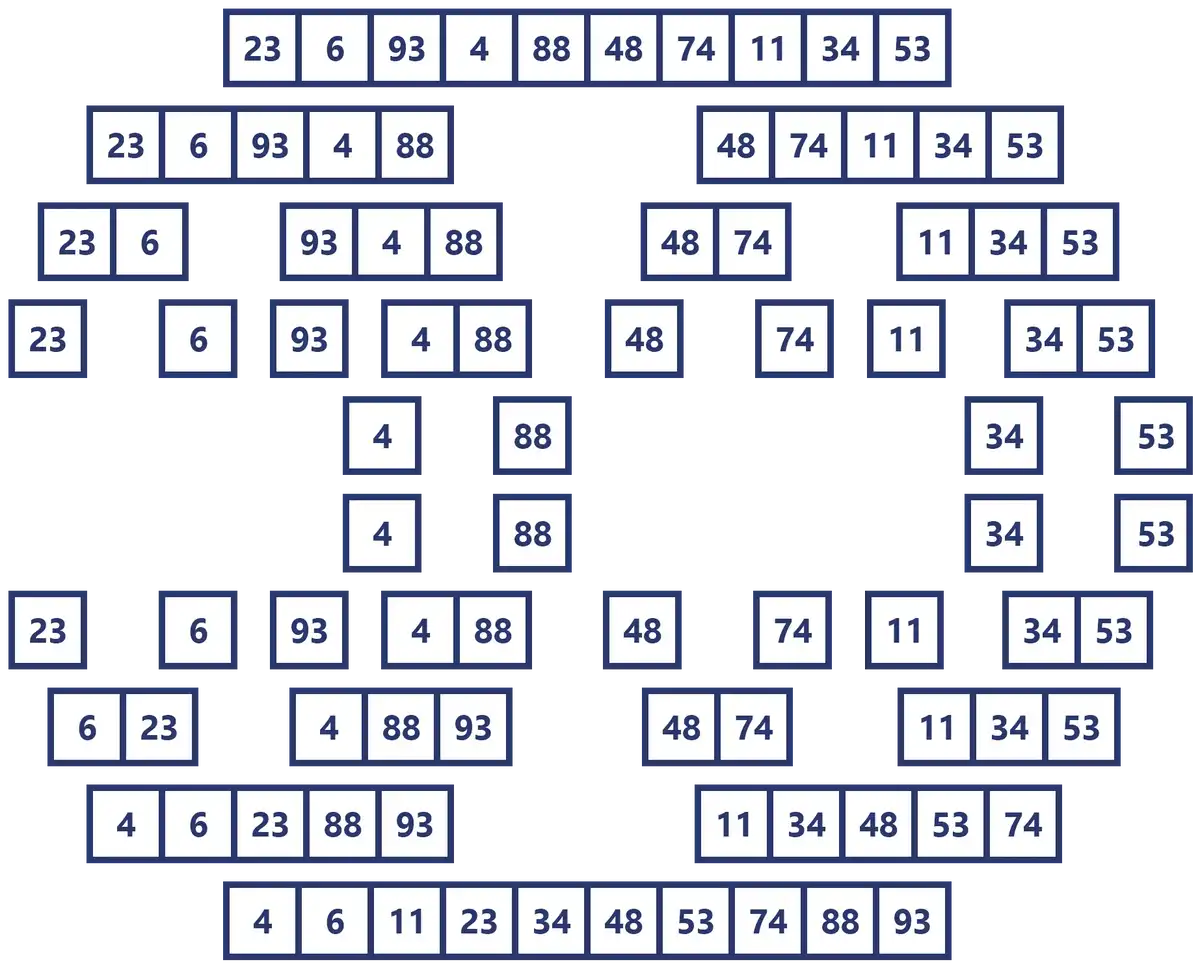
Suppose we have the following array of 10 numbers and we want to order them from smallest to largest:
Following the idea of “divide and conquer” we seek to divide the problem until we get to one so small that it can be solved trivially, so let’s start dividing the array in two.
Since it is an array of 10 elements and 10 divided by 2 is 5, we are going to have two arrays of 5 elements.
Ok, but the problem is still big and there is no trivial solution, so we continue to divide it.
In the next step we have to divide by 2 an array of 5 elements, as it is a decimal number we are going to take only the integer part (2), so we will have an array of 2 and another of 3 elements.
If we repeat this process until we can no longer simplify the problem, we will inevitably end up with 10 arrays of 1 element each.
Visually the whole process would look like this:
Let’s put it in code step by step
Before writing code I always ask myself these two questions.
What does our function need to do? Receive an array as a parameter and return it sorted.
What do we need to do? We need to split the array until we have a single element, and then sort it.
We have just defined our base case, that is, the condition to stop the recursion.
Let’s start by writing that. To avoid nested conditionals I’m going to write my code using Guard Clauses.
const mergeSort = (array) => {
// If our array has only one element, we no longer need to split it.
// This is our base case, we simply return the array.
if (array.length <= 1) return array
//
// Logic to sort the array...
//
}Now we have to divide the array in two, for that I used the slice() method proper of the arrays in JavaScript.
This method accepts two optional parameters, the first one is the initial position where it is going to start ‘copying’ the array, the second parameter is the final position.
If the second parameter is not specified, it will copy to the end of the array. And if no parameter is specified, the whole array will be copied.
The important thing about this method, unlike the ```splice()“ method, is that the latter modifies the original array.
Knowing how both methods work we can write our code as follows:
const mergeSort = (array) => {
if (array.length <= 1) return array
// middle is our "pivot", which is the element in the middle of the array
// Using ~~ is equivalent to Math.floor()
const middle = ~~(array.length / 2)
const left = array.slice(0, middle)
const right = array.slice(middle)
//
// Logic to sort the array...
//
}We have already divided the array in two, but we are missing the most important thing: the recursion.
And doing it is the simplest of all, but it can be the most abstract to understand.
We simply have to split the array in two again, and we already wrote all the logic to do it in this same function, so all we have to do is call ```mergeSort()“ again with the two halves of the array as parameter.
This code is going to be executed until we get to the base case, that is, until we have an array of 1 element.
const mergeSort = (array) => {
if (array.length <= 1) return array
const middle = ~~(array.length / 2)
// We call mergeSort() with the two halves of the array as parameter
const left = mergeSort(array.slice(0, middle))
const right = mergeSort(array.slice(middle))
//
// Logic to sort the array...
//
}How to recursively sort the array
We have already managed to divide our array as much as possible, now we have to sort the elements.
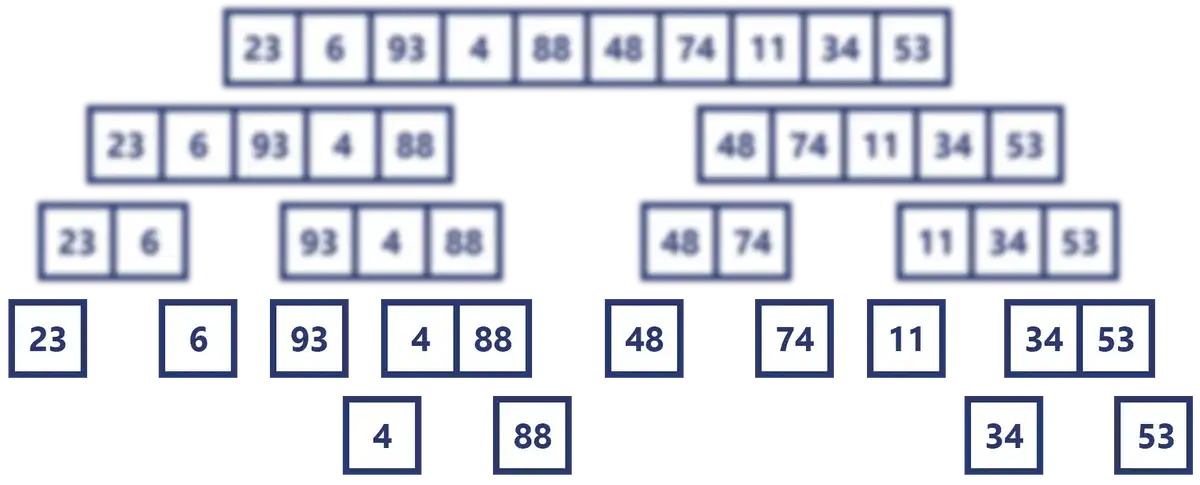
This indeed is the most abstract part of the recursion, so I want to graph it nicely so there’s not much room for confusion, so let’s go back to the last image and focus on the last two rows.
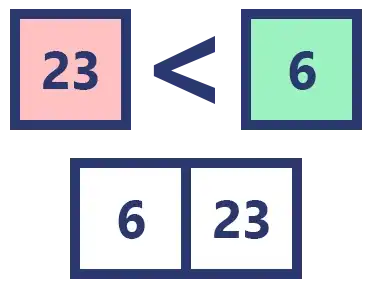
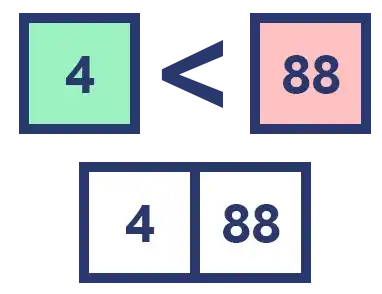
We can see that [23] and [6] are the first 1 element arrays, and they come just from splitting the array [23, 6], so [23] goes is the left part and [6] the right one.
Our mission now is to sort these two arrays and merge them back into one.
The logic to solve this is simple, we can create an array and go inserting the elements according to the order that we want, in this case we are going to do it in ascending order.
We compare 23 with 6. As 6 is less than 23 we insert it first, and as there are no more elements to compare we simply insert the 23 that is left over.
This case is the simplest, we are only comparing two elements, so let’s see one more example.
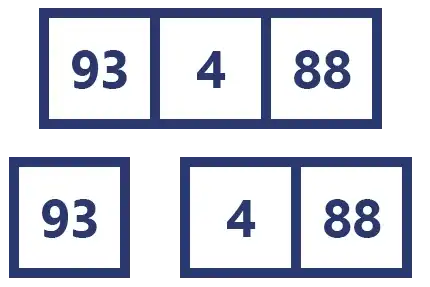
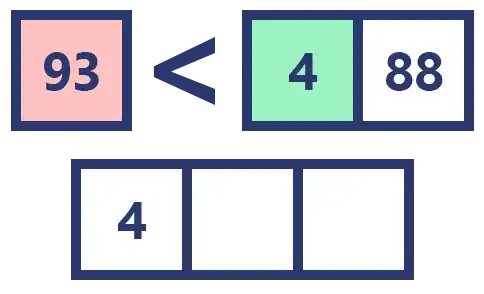
This time we have an array [93, 4, 48] that was split into two, [93] and [4, 48].
Following the logic of the previous example, we would have to compare the values inside each of the arrays to insert the smaller ones in a new array.
But actually the array [4, 48] has not finished splitting yet, remember that we are in a recursive function where the base case is that the array has only one element, so our function will split and sort this array before comparing it with another.
Exactly as before, we compare the values and insert them in order into a new array.
Coincidentally they were already sorted, but needless to say that this is not always the case, especially considering that the order (ascending or descending) is chosen by us.
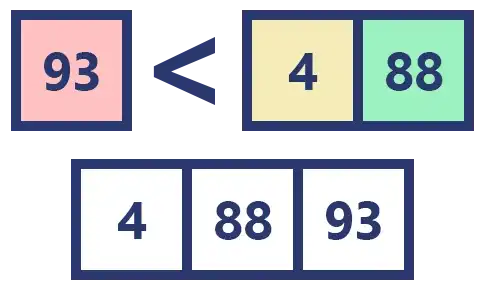
Now we can order these two arrays.
Although they are of different sizes, the sorting logic is always the same.
We compare the elements and insert them in order. 93 > 4, so we insert the 4 first.
When inserting it we can forget about that 4, we no longer have to compare it with any other element.
We move on to the next comparison. 93 > 88, so we insert the 88.
There are no more elements to compare, so we insert the leftover 93.
This process will be repeated until all the “pieces” of the array have been sorted and joined into one.
Understanding this process with code
We have already written our function ```mergeSort()“ which is in charge of splitting. Now we have to create another function to sort them, for that we are going to repeat the questions we asked ourselves before.
What does our function have to do? Receive two arrays as parameter and return an array with the elements of these sorted.
What do we need to do? We need to go through the arrays we received as parameters and compare the values of their elements to finally insert them in a new sorted array.
There are different ways to accomplish this task. One is using the shift() method, but this method as well as ````splice()``` modifies the array to which it is applied, so first I will explain how to do it without modifying the original array.
const sort = (left, right) => {
// I create an empty array that will store the elements in the correct order
const sortedArray = []
// I use these variables to know which index of the array I am traversing
let leftIndex = 0, rightIndex = 0
// As long as I have elements in at least one of the arrays I have to keep comparing elements
while (leftIndex < left.length && rightIndex < right.length) {
// I compare the elements of the arrangements
if (left[leftIndex] < right[rightIndex]) {
// I determined that the smallest number is left[leftIndex]
sortedArray.push(left[leftIndex])
// I no longer need to compare that number, so I increase its index by 1
leftIndex += 1
} else {
// I determined that the smallest number is right[rightIndex]
sortedArray.push(right[rightIndex])
// I no longer need to compare that number, so I increase its index by 1
rightIndex += 1
}
}
// And finally I return the ordered arrangement
return sortedArray
}By using the ```shift()“ method, which does modify the array to which it is applied, the code becomes shorter:
const sort = (left, right) => {
// I create an empty array that will store the elements in the correct order
const sortedArray = []
while (left.length > 0 && right.length > 0) {
// I search for the smallest element of the two arrays.
// The shift() method returns the first element of the array and removes it from the original one.
// That's why the while condition is that at least one of the two arrays has elements.
if (left[0] < right[0]) sortedArray.push(left.shift())
else sortedArray.push(right.shift())
}
// Finally I return the ordered arrangement
return sortedArray
}These codes work fine, but there is a problem.
In both cases the exit condition of the iteration is that we have finished traversing one of the arrays.
This means that there are still elements left in the array that we did not finish traversing.
Fortunately we don’t have to think too much about what to do with the rest of the elements. By the logic of our recursive algorithm it is certain that the elements we have not traversed are in the correct order (as we saw with images in the second example), so we just have to add them to the already sorted array.
We can do this by simply concatenating the arrays through the method concat() , but from the point where we stop exploring them, something we know thanks to the value of the leftIndex and rightIndex variables.
In code it would look like this:
const sort = (left, right) => {
const sortedArray = []
let leftIndex = 0, rightIndex = 0
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] < right[rightIndex]) {
sortedArray.push(left[leftIndex])
leftIndex += 1
} else {
sortedArray.push(right[rightIndex])
rightIndex += 1
}
}
// One of the two is going to be an empty array.
// But we are not interested in discarding it, so we concatenate both of them
return sortedArray.concat(left.slice(leftIndex)).concat(right.slice(rightIndex))
}If we did not care to modify the original array we can do it as we did in the previous code but without passing any parameter to slice().
Or we can use ”array destructuring”, as follows:
const sort = (left, right) => {
const sortedArray = []
while (left.length > 0 && right.length > 0) {
if (left[0] < right[0]) sortedArray.push(left.shift())
else sortedArray.push(right.shift())
}
// Again, one of the two arrays will be empty.
// But it is precisely because it is empty that it is not necessary to discard it.
return [...sortedArray, ...left, ...right]
}And with these two simple functions we would already have the necessary pieces to implement Merge Sort in JavaScript.
At the end the process that our code will follow will look something like this:
The complete code in case you do not want to modify the original sort is:
const mergeSort = (array) => {
if (array.length <= 1) return array
const middle = ~~(array.length / 2)
const left = mergeSort(array.slice(0, middle))
const right = mergeSort(array.slice(middle))
return sort(left, right)}
const sort = (left, right) => {
const sortedArray = []
let leftIndex = 0, rightIndex = 0
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] < right[rightIndex]) {
sortedArray.push(left[leftIndex])
leftIndex += 1
} else {
sortedArray.push(right[rightIndex])
rightIndex += 1
}
}
return sortedArray.concat(left.slice(leftIndex)).concat(right.slice(rightIndex))
}And the complete code in case we do not mind modifying the original arrangement is:
const mergeSort = (array) => {
if (array.length <= 1) return array
const middle = ~~(array.length / 2)
const left = mergeSort(array.slice(0, middle))
const right = mergeSort(array.slice(middle))
return sort(left, right)}
const sort = (left, right) => {
const sortedArray = []
while (left.length > 0 && right.length > 0) {
if (left[0] < right[0]) sortedArray.push(left.shift())
else sortedArray.push(right.shift())
}
return [...sortedArray, ...left, ...right]
}In both cases we must not forget to call the sort() function inside the mergeSort() function.
Why use Merge Sort?
The advantage of Merge Sort over other more basic sorting algorithms is its short runtime.
It is one of the fastest and most efficient sorting algorithms, with a Big-Θ of Θ(n*log(n)) even in the worst case.
What is the worst case?
When running Merge Sort we don’t necessarily have to compare all the elements to sort them, because when we finish traversing and sorting a subarray (the exit condition of our loop) we can take for granted that the rest of the elements are already sorted and group them (i.e., concatenate them as in our code).
With this in mind we can infer that the worst case will be when our algorithm has to do all possible comparisons.
An example would be the array [0, 2, 4, 6, 1, 3, 5, 7].
You can do the process on this page and you will see that the algorithm will always have to compare the elements with each other in order to sort them.
When to use Merge Sort?
There is an important part of this algorithm that we have been doing, and that is that in order to get it to work we are creating new arrays where we insert the elements in the desired order.
**This can be a problem if we are dealing with a huge amount of data and it may be better to use another algorithm such as Quick Sort or Heap Sort.
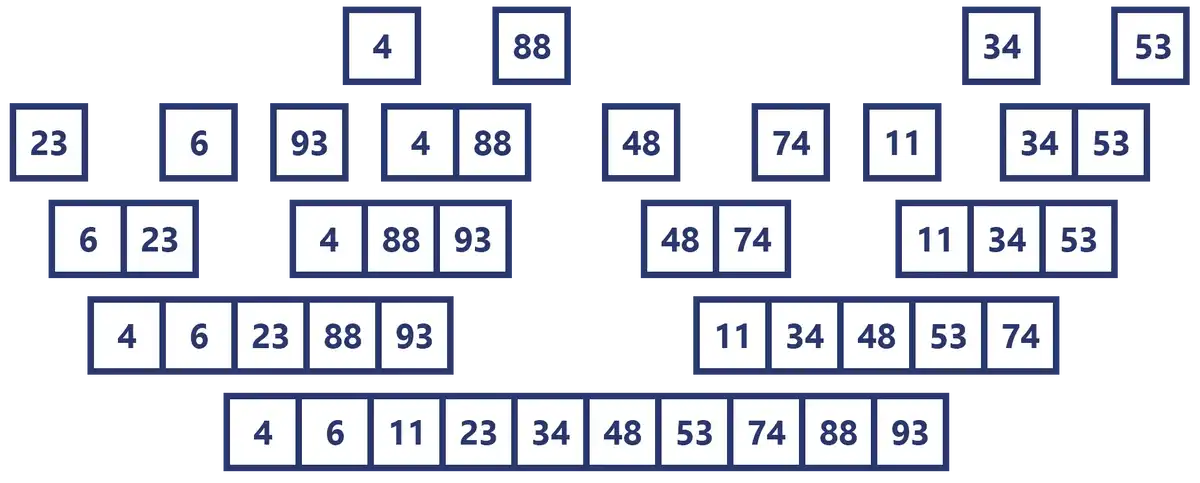
The complete process of the Merge Sort algorithm in one image
While I was making this article I ended up with an image of this rather curious shape, so I share it to finish the topic.
Conclusion
Merge Sort is a very efficient sorting algorithm even in the worst case, but it requires a lot of extra memory space to work. This makes it not a very good choice when dealing with a large amount of data; but in the opposite case it is an excellent alternative in contrast to the other sorting algorithms.